Induktor dan Kapasitor dalam Domain Laplace
Salah satu kegunaan transformasi model induktor dan kapasitor ke domain \(s\) berguna adalah untuk menyederhanakan analisis rangkaian, terutama rangkaian orde dua. Dalam domain \(s\), operasi derivative bisa dihindari dan digantikan dengan operasi aljabar biasa.
Induktor
Hubungan tegangan-arus induktor dalam domain \(t\):
\[\begin{equation} v_L(t)=L\frac{di_L(t)}{dt} \end{equation}\]Operasi transformasi Laplace terhadap (1):
\[\begin{equation}\begin{split} V_L(s)&=L\left[sI_L(s)-i_L(0^-)\right]\\ &=sLI_L(s)-Li_L(0^-) \end{split}\end{equation}\]dimana \(i_L(0^-)\) adalah arus inisial induktor.
Ekivalensi rangkaian seri induktor berdasarkan (2):
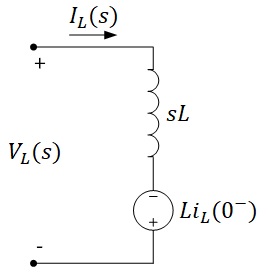
Persamaan (2) bisa juga diubah ke bentuk berikut:
\[\begin{equation}\begin{split} sLI_L(s)&=V_L(s)+Li_L(0^-)\\ I_L(s)&=\frac{V_L(s)}{sL}+\frac{i_L(0^-)}{s} \end{split}\end{equation}\]Ekivalensi rangkaian paralel induktor berdasarkan (3):
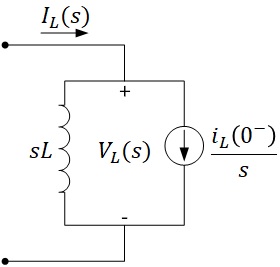
Kapasitor
Hubungan tegangan-arus kapasitor dalam domain \(t\):
\[\begin{equation} i_C(t)=C\frac{dv_C(t)}{dt} \end{equation}\]Operasi transformasi Laplace terhadap (4):
\[\begin{equation}\begin{split} I_C(s)&=C\left[sV_C(s)-v_C(0^-)\right]\\ &=sCV_C(s)-Cv_C(0^-) \end{split}\end{equation}\]dimana \(v_C(0^-)\) adalah tegangan inisial kapsitor.
Ekivalensi rangkaian paralel kapasitor berdasarkan (5):
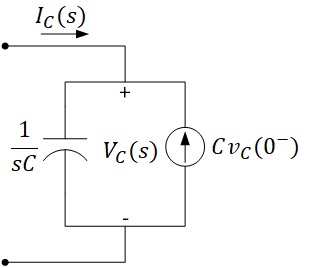
Persamaan (5) bisa juga diubah ke bentuk berikut:
\[\begin{equation}\begin{split} sCV_C(s)&=I_C(s)+Cv_C(0^-)\\ V_C(s)&=\frac{I_C(s)}{sC}+\frac{v_C(0^-)}{s} \end{split}\end{equation}\]Ekivalensi rangkaian seri kapasitor berdasarkan (6):
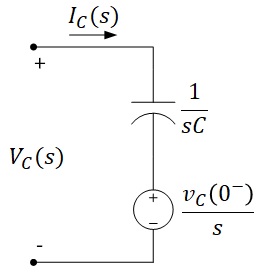
---
Blog archive: Years / Categories / Tags