Linearisasi Perkalian Dua Variabel Kontinyu
Di tulisan sebelumnya, kita telah belajar bagaimana melakukan linearisasi perkalian antara variabel biner dan variable kontinyu. Kali ini kita beralih ke ragam berikutnya: perkalian antara dua variabel kontinyu. Perkalian antara dua variabel kontinyu tentu saja lebih rumit.
Berbeda dengan linearisasi pada perkalian antara variabel biner dan variabel kontinyu, linearisasi pada perkalian antara dua variabel kontinyu tidak bisa dilakukan secara eksak. Maksudnya, hasil linearisasi tidaklah 100% mewakili ekspresi aslinya, ada sekian persen galat (error). Meskipun demikian, linearisasi ini tetap sangat worth it untuk dilakukan. Salah satu contoh aplikasinya adalah dalam dunia optimisasi, dimana ekspresi perkalian antara dua variabel kontinyu banyak dijumpai baik dalam fungsi objektif maupun dalam fungsi pengekangnya.
Teori
Linearisasi perkalian dua variabel kontinyu dilakukan dengan terlebih dahulu mengubah ekspresi asli ke bentuk separable function, yakni jumlahan dari fungsi variabel skalar. Misalkan kita mempunyai ekspresi \(x_1x_2\), dimana \(x_1,x_2\in\mathbb{R}\). Secara matematis, ekivalensi ekspresi \(x_1x_2\) dengan separable function-nya dapat ditulis sebagai berikut.
\[\begin{equation} x_1x_2=f(y_1)+f(y_2) \end{equation}\]dimana \(y_1\) dan \(y_2\) adalah variabel-variabel baru yang kita definisikan untuk konstruksi separable function ini.
Jadi, langkah pertama yang perlu dilakukan adalah mendefinisikan variabel \(y_1\) dan \(y_2\). Hubungan antara \(y_1\) dan \(y_2\) dengan variabel asli \(x_1\) dan \(x_2\) adalah sebagai berikut.
\[\begin{equation} y_1=\frac{1}{2}(x_1+x_2) \end{equation}\] \[\begin{equation} y_2=\frac{1}{2}(x_1-x_2) \end{equation}\]Dengan menggunakan (2) dan (3), ekspresi \(x_1x_2\) dapat dinyatakan sebagai berikut.
\[\begin{equation} x_1x_2=y_1^2-y_2^2 \end{equation}\]Perhatikan bahwa (4) adalah separable function yang mengikuti pola di (1). Apabila batas bawah dan batas atas untuk \(x_1\) dan \(x_2\) masing-masing adalah \((x_{1,\min},x_{1,\max})\) dan \((x_{2,\min},x_{2,\max})\), batas-batas untuk \(y_1\) dan \(y_2\) dapat dengan mudah dihitung sebagai berikut.
\[\begin{equation} \frac{1}{2}(x_{1,\min}+x_{2,\min})\leq y_1\leq \frac{1}{2}(x_{1,\max}+x_{2,\max}) \end{equation}\] \[\begin{equation} \frac{1}{2}(x_{1,\min}-x_{2,\max})\leq y_2\leq \frac{1}{2}(x_{1,\max}-x_{2,\min}) \end{equation}\]Setelah konversi ke separable function dilakukan dan batas-batas variabel baru \(y_1\) dan \(y_2\) juga sudah dihitung, linearisasi dapat dengan mudah dilakukan secara individual terhadap \(y_1^2\) dan \(y_2^2\) menggunakan teknik piecewise linearization. Dalam teknik ini, \(y_1^2\) dan \(y_2^2\) masing-masing direpresentasikan menggunakan beberapa segmen garis lurus dengan gradien (slope) yang berbeda.
Sebagai contoh, kita akan melakukan linearisasi fungsi kuadrat menggunakan 3 segmen garis lurus. Perhatikan ilustrasinya pada gambar berikut.
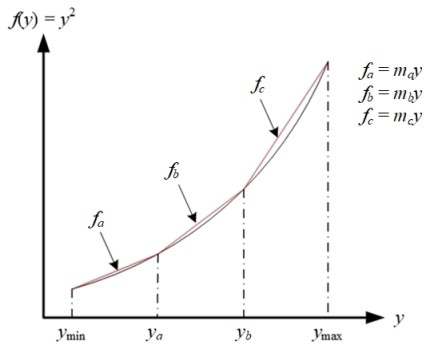
Fungsi yang akan kita linearkan adalah \(f(y)=y^2\). Tiga segmen garis lurus untuk linearisasi kita beri notasi \(f_a,f_b\), dan \(f_c\), masing-masing dengan gradien \(m_a,m_b\), dan \(m_c\). Untuk bisa membentuk persamaan segmen-segmen garis lurus tersebut, yang perlu kita lakukan adalah menghitung \(m_a,m_b\), dan \(m_c\). Bisa kita observasi dari gambar bahwa nilai \(m_a,m_b\), dan \(m_c\) bisa dihitung sebagai berikut.
\[\begin{equation} m_a=\frac{y_a^2-y_\min^2}{y_a-y_\min} \end{equation}\] \[\begin{equation} m_b=\frac{y_b^2-y_a^2}{y_b-y_a} \end{equation}\] \[\begin{equation} m_c=\frac{y_\max^2-y_b^2}{y_\max-y_b} \end{equation}\]dimana \(y_a\) dan \(y_b\) masing-masing adalah titik peralihan antara segmen garis ke segmen garis kedua dan segmen garis kedua ke segmen garis ketiga. Pembagian region pada sumbu horisontal tidak harus sama rata, dalam artian persamaan \(y_a-y_\min=y_b-y_a=y_\max-y_b\) tidak harus terpenuhi.
Setelah semua gradien terhitung, the job is basically done. Jadi fungsi \(f(y)\) bisa kita aproksimasi dengan ekspresi linear berikut.
\[\begin{equation} f(y)=y^2\approx \begin{cases} m_ay \hspace{15pt} y_\min\leq y\leq y_a\\ m_by \hspace{15pt} y_a\leq y\leq y_b\\ m_cy \hspace{15pt} y_b\leq y\leq y_\max \end{cases} \end{equation}\]Semakin banyak segmen garis lurus yang kita pakai, ekspresi linear yang kita hasilkan semakin mendekati ekspresi aslinya. Konsekuensi yang muncul tentu beban komputasi yang bertambah.
Contoh Aplikasi
Misalkan dalam sebuah optimisasi kita memiliki fungsi pengekang sebagai berikut.
\[\begin{equation} x_1x_2\leq 10 \end{equation}\]dimana \(0\leq x_1\leq 9\), \(0\leq x_2\leq 12\), dan \(x,y\in\mathbb{R}\). Kita akan melakukan linearisasi pada ekspresi ini.
Langsung saja, langkah pertama adalah mendefinisikan variabel baru \(y_1\) dan \(y_2\) dan kemudian menghitung batas-batasnya menggunakan (5) dan (6):
\[\begin{split} y_{1,\min}&=\frac{1}{2}(0+0)=0\\ y_{1,\max}&=\frac{1}{2}(9+12)=\frac{21}{2}\\ y_{2,\min}&=\frac{1}{2}(0-12)=-6\\ y_{2,\max}&=\frac{1}{2}(9-0)=\frac{9}{2} \end{split}\]Langkah kedua adalah melakukan linearisasi terhadap \(y_1^2\) dan \(y_2^2\) di (4) menggunakan piecewise linearization. Misalkan kita menggunakan 3 segmen garis linear sebagaimana ada gambar di atas. Dengan asumsi pembagian region sumbu horisontal yang sama lebar, titik-titik peralihan untuk \(y_1\) adalah
\[\begin{split} y_{1a}&=0+\frac{1}{3}(21/2-0)=\frac{7}{2}\\ y_{1b}&=0+\frac{2}{3}(21/2-0)=7 \end{split}\]Sedangkan titik-titik peralihan untuk \(y_2\) adalah
\[\begin{split} y_{2a}&=-6+\frac{1}{3}(9/2-(-6))=-\frac{5}{2}\\ y_{2b}&=-6+\frac{2}{3}(9/2-(-6))=1 \end{split}\]Setelah titik-titik peralihan diketahui, gradien segmen-segmen garis lurus bisa dengan mudah kita hitung. Untuk \(f(y_1)\), gradien-gradiennya adalah
\[\begin{split} m_{1a}&=\frac{(7/2)^2-0^2}{7/2-0}=\frac{7}{2}\\ m_{1b}&=\frac{7^2-(7/2)^2}{7-(7/2)}=\frac{21}{2}\\ m_{1c}&=\frac{(21/2)^2-7^2}{(21/2)-7}=\frac{35}{2} \end{split}\]Sedangkan untuk \(f(y_2)\), gradien-gradiennya adalah
\[\begin{split} m_{2a}&=\frac{(-5/2)^2-(-6)^2}{(-5/2)-(-6)}=-\frac{17}{2}\\ m_{2b}&=\frac{1^2-(-5/2)^2}{1-(-5/2)}=-\frac{3}{2}\\ m_{2c}&=\frac{(9/2)^2-1^2}{(9/2)-1}=\frac{11}{2} \end{split}\]Dari nilai gradien-gradien ini, aproksimasi \(f(y_1)\) dan \(f(y_2)\) kita konstruksikan sebagai berikut.
\[f(y_1)=y_1^2\approx \begin{cases} \frac{7}{2}y_1 \hspace{15pt} &0\leq y_1\leq 7/2\\ \frac{21}{2}y_1 \hspace{15pt} &7/2\leq y_1\leq 7\\ \frac{35}{2}y_1 \hspace{15pt} &7\leq y_1\leq 21/2 \end{cases}\] \[f(y_2)=y_2^2\approx \begin{cases} -\frac{17}{2}y_2 \hspace{15pt} &-6\leq y_2\leq -5/2\\ -\frac{3}{2}y_2 \hspace{15pt} &-5/2\leq y_2\leq 1\\ \frac{11}{2}y_2 \hspace{15pt} &1\leq y_2\leq 9/2 \end{cases}\]Langkah terakhir, substitusikan aproksimasi ini ke ekspresi
\[y_1^2-y_2^2\leq 10\]Ingat bahwa ekspresi ini ekivalen dengan ekspresi awal \(x_1x_2\leq 10\).
Selamat mencoba…
---
Blog archive: Years / Categories / Tags