Perkalian antara Skalar dan Vektor

Operasi perkalian pada vektor terbagi menjadi 2 macam, yaitu perkalian antara vektor dan skalar dan perkalian sesama vektor. Jenis perkalian pertama tentu lebih mudah dibanding yang kedua. Oleh karena itu, mari kita mulai dari yang paling mudah. Di edisi ini, kita akan belajar perkalian skalar-vektor dan sifat-sifatnya, disertai dengan contoh penjelas.

Teori Dasar

Perkalian skalar-vektor dilakukan dengan mengalikan setiap elemen vektor dengan skalar pengalinya. Dalam penulisannya, skalar bisa diletakkan di sebelah kiri maupun di sebelah kanan tanpa mempengaruhi hasil perkalian. Berikut ini beberapa contoh perkalian skalar-vektor,

\[(3) \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}= \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix} (3)= \begin{bmatrix} 6\\ 12\\ 18\\ \end{bmatrix}\]

Selain dengan skalar berupa bilangan bulat positif, vektor bisa juga dikalikan dengan bilangan negatif, contohnya

\[(-2) \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}= \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}(-2)= \begin{bmatrix} -4\\ -8\\ -12\\ \end{bmatrix}\]

atau dengan pecahan, misalnya

\[\left(\frac{1}{2}\right) \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}= \begin{bmatrix} 1\\ 2\\ 3\\ \end{bmatrix}= \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}/2\]

Bahkan bisa dikalikan juga dengan nol, contohnya

\[(0) \begin{bmatrix} 2\\ 4\\ 6\\ \end{bmatrix}= \begin{bmatrix} 0\\ 0\\ 0\\ \end{bmatrix}=0\]

Next, kita akan jelaskan bahwa perkalian skalar-vektor mengikuti/mempunyai beberapa sifat (satu diantaranya sudah tersirat dari contoh di atas). Misalkan kita memiliki sebuah vektor \(x\) dan beberapa skalar, katakanlah \(\alpha\), \(\beta\), dan \(\gamma\), maka sifat-sifat perkalian skalar-vektor dapat dijelaskan sebagai berikut:

Sifat Komutatif

Sifat komutatif perkalian skalar-vektor dinyatakan sebagai berikut,

\[\alpha x=x\alpha\]

Hal ini berarti bahwa susunan vektor dan skalar dapat dibolak-balik, sebagaimana contoh di atas.

Sifat Asosiatif

Sifat asosiatif perkalian skalar-vektor terdefinisikan sebagai berikut,

\[(\beta\gamma)x=\beta(\gamma x)\]

Dengan kata lain, dua ekspresi di atas sama dengan \(\beta\gamma x\). Sifat asosiatif juga bisa dinyatakan melalui ekspresi berikut,

\[\beta(\gamma x)=(\beta x)\gamma\]

Dari sini kita tahu bahwa \(\beta\gamma x=\beta x\gamma\).

Sifat Distributif

Sifat distributif perkalian skalar-vektor terbagi menjadi 2, yaitu sifat distributif kiri dan sifat distributif kanan. Sifat distributif kiri yaitu

\[(\beta+\gamma)x=\beta x+\gamma x\]

Ingat bahwa operasi perkalian lebih kuat dibanding penjumlahan, maka \(\beta x+\gamma x\) sama dengan \((\beta x)+(\gamma x)\). Menarik untuk kita observasi bahwa dua tanda \(+\) di atas merupakan dua penjumlahan berbeda. Tanda \(+\) di sebelah kiri tanda sama dengan merepresentasikan penjumlahan skalar, sementara tanda \(+\) di sebelah kanan tanda sama dengan merepresentasikan penjumlahan vektor.

Pada ekspresi \((\beta+\gamma)x\) di atas, skalar terletak di sebelah kiri. Apabila skalar terletak di sebelah kanan, kita akan mempunyai sifat distributif kanan, yaitu

\[x(\beta+\gamma)=x\beta+x\gamma\]

Misalnya kita punya vektor lain, katakanlah vektor \(y\), maka sifat distributif kanan bisa juga dinyatakan sebagai berikut,

\[\beta(x+y)=\beta x+\beta y\]

Sampai di sini, saya reminder lagi bahwa \(x\) dan \(y\) adalah dua vektor dengan ukuran yang sama, meskipun elemennya bisa berbeda, sementara \(\alpha\), \(\beta\), dan \(\gamma\) adalah skalar.

Contoh Perkalian Skalar-Vektor

Contoh perkalian skalar-vektor dapat kita temukan kembali di kasus perpindahan sebuah benda. Perpindahan benda kita nyatakan sebagai vektor \(x\). Apabila \(x\) kita kalikan bilangan/skalar \(\beta\), dimana \(\beta>0\), maka vektor \(\beta x\) merupakan perpindahan dengan arah yang sama dengan \(x\) tetapi dengan magnitudo yang di-scaling sebesar \(\beta\). Apabila \(\beta<0\), berarti kita membalik arah perpindahan sekaligus men-scaling magnitudo-nya sebesar \(\vert\beta\vert\). Lihat Gambar 1 untuk ilustrasinya.

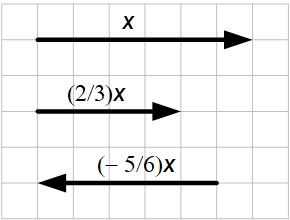
Gambar 1. Ilustrasi perkalian skalar-vektor: vektor asli x (atas), scaling vektor x sebesar 2/3 (tengah), dan pembalikan arah vektor x sekaligus scaling sebesar 5/6

Kombinasi Linear Vektor

Dari penjelesan sebelumnya kita telah paham bahwa perkalian skalar-vektor pada dasarnya adalah proses scaling terhadap sebuah vektor. Dalam aljabar linear, penjumlahan beberapa vektor yang telah di-scaling ini disebut kombinasi linear vektor. Apabila kita mempunyai set vektor \(x_1,\dots,x_m\) dan set skalar \(\beta_1,\dots,\beta_m\), ekspresi berikut

\[\beta_1x_1+...+\beta_mx_m\]

adalah kombinasi linear dari set vektor \(x_1,\dots,x_m\). Set skalar \(\beta_1,\dots,\beta_m\) dinamakan koefisien dari kombinasi linear tersebut. Kombinasi linear merupakan konsep yang sangat penting dan akan banyak dipakai dalam topik-topik berikutnya.

Salah satu hal unik berkaitan dengan kombinasi linear ini adalah bahwa vektor apapun bisa dinyatakan sebagai kombinasi linear dari vektor-vektor unit. Misalnya kita mempunyai vektor \(y\) dengan \(n\) elemen, maka vektor \(y\) bisa dinyatakan sebagai kombinasi linear \(n\) vektor unit berikut,

\[y=y_1e_1+...+y_ne_n\]

Perhatikan bahwa \(y_1,...,y_n\) adalah elemen-elemen dari vektor \(y\), atau dengan kata lain mereka adalah skalar, sedangkan \(e_i\) \((i=1,\dots,n)\) adalah vektor unit ke-\(i\). Jadi dalam kombinasi linear di atas, koefisien-nya adalah elemen-elemen vektor \(y\). Contohnya adalah sebagai berikut,

\[\begin{bmatrix} 3\\ -2\\ 5\\ \end{bmatrix}= 3\begin{bmatrix} 1\\ 0\\ 0\\ \end{bmatrix}+ (-2)\begin{bmatrix} 0\\ 1\\ 0\\ \end{bmatrix}+ 5\begin{bmatrix} 0\\ 0\\ 1\\ \end{bmatrix}\]

Koefisien \(\beta_1,\dots,\beta_m\) pada sebuah kombinasi linear bisa saja mempunyai nilai tertentu yang menjadikan kombinasi linear tersebut spesial. Nilai-nilai spesial tersebut adalah sebagai berikut,

Apabila \(\beta_1=\dots=\beta_m=1\), kombinasi linear-nya akan menjadi \(x_1+\dots+x_m\), maka yang kita peroleh adalah jumlahan dari set vektor \(x_1,\dots,x_m\)
Apabila \(\beta_1=\dots=\beta_m=1/m\), kombinasi linear-nya akan menjadi \((1/m)(x_1+\dots+x_m)\), maka yang kita peroleh adalah rata-rata dari set vektor \(x_1,\dots,x_m\)
Apabila \(\beta_1+\dots+\beta_m=1\), kombinasi linear yang kita peroleh dinamakan kombinasi affine. Untuk \(\beta_1,\dots,\beta_m\) yang bernilai non-negatif, kombinasi affine yang diperoleh disebut juga kombinasi convex, bauran (mixture), atau rata-rata dengan pembobotan (weighted average)

Kembali kita gunakan vektor perpindahan sebagai contoh kombinasi linear vektor. Gambar 2 mengilustrasikan kombinasi linear sebagai jumlahan dari vektor-vektor perpindahan yang telah di-scaling.