Mengenal Vektor
Dalam aljabar linear, pembahasan mengenai vektor merupakan konsep dasar yang sangat krusial karena menjadi building block bagi konsep-konsep selanjutnya yang lebih rumit. Jika konsep vektor berhasil dikuasai, insya Allah pembahasan selanjutnya akan lebih mudah dipahami. Karena itu, artikel mengenai pengenalan vektor ini saya letakkan persis setelah tulisan pembukaan.
1. Definisi Array
Sebelum membahas vektor, kita perlu mendiskusikan array terlebih dahulu. Apa hubungan antara array dan vektor? Simpelnya, array adalah generalisasi dari vektor. Array adalah kumpulan angka yang disusun dalam urutan tertentu. Dalam praktiknya, array dituliskan sebagai kumpulan angka yang ditutup dengan kurung. Array bisa berdimensi satu, contohnya
\[\begin{bmatrix} 1,2,3\\ \end{bmatrix}\]Bisa juga berdimensi dua, contohnya
\[\begin{bmatrix} 1 & 5\\ 3 & 7\\ 4 & 8\\ \end{bmatrix}\]Bisa dipahami perbedaannya ya? Kalau belum paham juga, coba bayangkan sekumpulan tentara yang sedang berbaris membentuk sekian saf dan sekian banjar. Array 1 dimensi bisa dianalogikan dengan barisan tentara yang hanya terdiri dari 1 saf atau 1 banjar. Nah, kalau barisan tentaranya tersusun dari lebih dari 1 saf dan lebih dari 1 banjar berarti analoginya adalah array 2 dimensi. Jika di baris berbaris istilahnya adalah “saf” dan “banjar”, di array istilahnya adalah “baris” dan “kolom”. Jadi, array 2 dimensi di atas memiliki 3 baris dan 2 kolom.
Namun, dimensi array tidak terbatas hanya pada angka 2. Array bisa berdimensi lebih dari 2, tanpa dibatasi angka maksimal tertentu. Sayangnya, kalau dimensi array sudah lebih dari 2 seperti ini, kita tidak bisa lagi menggunakan analogi barisan tentara 😐.
2. Definisi Vektor
Nah, jika konsep array sudah dipahami, definisi vektor pun akan lebih mudah dicerna. Vektor tidak lain adalah array 1 dimensi, namun dengan pembedaan susunan angka-angkanya (angka-angka penyusun vektor disbut juga elemen vektor). Maksudnya, vektor yang tersusun dari 1 baris angka/elemen akan dianggap berbeda dengan vektor yang tersusun dari 1 kolom angka/elemen, meskipun angka-angkanya sama. Sebagai contoh, vektor 1 kolom berikut
\[\begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\]tidak sama dengan vektor 1 baris berikut
\[\begin{bmatrix} 1 & 2 & 3 & 4\\ \end{bmatrix}\]meskipun angka-angkanya sama. Vektor pertama disebut vektor kolom dan vektor kedua disebut vektor baris.
Untuk identifikasi, vektor diberi nama dengan sebuah huruf kecil. Ada beberapa variasi dalam penulisannya. Misalnya sebuah vektor kita beri nama “a”. Maka, huruf “a” bisa ditulis dalam 3 cara: (i) ditulis apa adanya tetapi dimiringkan, yaitu \(a\), (ii) ditulis menggunakan huruf tebal tanpa dimiringkan, yaitu \(\mathbf{a}\), atau (iii) dengan memberikan tanda panah di atas huruf, yaitu \(\vec{a}\). Saya pribadi lebih suka menggunakan cara penulisan pertama karena lebih simpel dibanding cara kedua dan ketiga. Karena itu, ke depannya saya akan konsisten dengan metode penulisan pertama. Untuk membedakan antara vektor dengan skalar, skalar biasanya diberi simbol dengan aksara Yunani (\(\alpha\), \(\beta\), …).
By default, jika kita menyebut sebuah vektor tertentu, maka yang dimaksud adalah vektor kolom. Sebagai contoh, kita mempunyai vektor \(a\) yang elemen-nya adalah 1, 2, 3, and 4. Maka, penulisan vektor \(a\) adalah
\[a= \begin{bmatrix} 1\\ 2\\ 3\\ 4\\ \end{bmatrix}\]Untuk menghemat tempat, vektor \(a\) bisa juga dituliskan seperti berikut,
\[a= \begin{pmatrix} 1,2,3,4\\ \end{pmatrix}\]Vektor yang hanya memiliki 1 elemen saja, maka normalnya tidak kita katakan sebagai vektor, tapi cukup kita sebut sebagai skalar saja dan penulisannya pun tidak perlu memakai kurung. Jadi, elemen penyusun vektor adalah skalar.
Untuk menyebut/mengakses elemen vektor tertentu, digunakan indeksasi. Indeksasi bisa dilakukan dengan huruf apapun, tapi yang paling umum adalah \(i\). Mari kita lihat bagaiman indeksasi untuk vektor \(a\) di atas. Karena \(a\) tersusun dari 4 elemen, \(i=1,2,3,4\). Maka, untuk vektor \(a\), elemen pertamanya adalah \(a_1=1\), elemen keduanya adalah \(a_2=2\), elemen ketiganya adalah \(a_3=3\), dan elemen keempatnya adalah \(a_4=4\).
Lebih jauh, elemen-elemen vektor bisa berupa bilangan riil, seperti pada vektor \(a\) di atas, atau bisa juga berupa bilangan kompleks. Vektor dengan elemen bilangan riil saja kita sebut sebagai vektor riil, sementara vektor dengan elemen bilangan kompleks kita sebut sebagai vektor kompleks. Dalam aplikasi di dunia nyata, vektor riil lebih sering muncul dibanding vektor kompleks. Karenanya, mayoritas yang akan diskusikan di sini (dan di catatan-catatan selanjutnya) adalah vektor riil.
Set bilangan riil biasa dituliskan dengan \(\mathbb{R}\) dan sebuah vektor yang tersusun dari \(n\) bilangan riil dinotasikan dengan \(\mathbb{R}^n\). Misalnya, vektor \(a\) di atas tersusun dari 4 bilangan riil, maka vektor \(a\) bisa dituliskan juga \(a\in\mathbb{R}^4\). Jadi, notasi \(a\in\mathbb{R}^n\) bermakna bahwa vektor \(a\) adalah elemen dari set \(\mathbb{R}^n\).
3. Vektor Blok dan Sub Vektor
Sebuah vektor terkadang pula dinyatakan sebagai susunan dari vektor-vektor lain. Vektor seperti ini dinamakan vektor blok. Sebagai contoh, lihat vektor \(v\) berikut,
\[v= \begin{bmatrix} x\\ y\\ z\\ \end{bmatrix} = \begin{pmatrix} x,y,z \end{pmatrix}\]Perhatikan bahwa vektor \(v\) tersusun dari \(x\), \(y\), dan \(z\) yang juga merupakan vektor. Jika vektor \(x\) tersusun dari \(m\) elemen skalar, \(y\) tersusun dari \(n\) elemen skalar, dan \(z\) tersusun dari \(p\) elemen skalar, vektor \(v\) di atas bisa kita jabarkan sebagai berikut,
\[v= \begin{pmatrix} x_1,x_2,...,x_m,y_1,y_2,...,y_n,z_1,z_2,...,z_p\\ \end{pmatrix}\]Maka kita katakan bahwa vektor \(v\) ini adalah vektor blok. Apakah vektor blok hanya boleh tersusun dari vektor saja? Jawabannya: tidak. Vektor blok boleh juga disusun dari skalar dan vektor sekaligus, contohnya
\[w= \begin{bmatrix} 5\\ x\\ y\\ z\\ \end{bmatrix}\]Next, perhatikan kembali vektor \(v\) di atas. Vektor \(v\) tersusun dari vektor-vektor lain, yaitu \(x\), \(y\), dan \(z\). Oleh karena itu, vektor-vektor \(x\), \(y\), dan \(z\) ini bisa juga kita katakan sebagai sub vektor dari \(v\). Notasi “rentang” bisa kita gunakan untuk menyatkan \(x\), \(y\), dan \(z\). Ingat bahwa elemen vektor \(x\) adalah elemen ke-1 hingga ke-\(m\) dari \(v\), elemen vektor \(y\) adalah elemen ke-\((m+1)\) hingga ke-\((m+n)\) dari \(v\), dan elemen vektor \(z\) adalah elemen ke-\((m+n+1)\) hingga ke-\((m+n+p)\) dari \(v\). Maka
\[\begin{split} &x=v_{1:m}\\ &y=v_{(m+1):(m+n)}\\ &z=v_{(m+n+1):(m+n+p)} \end{split}\]4. Vektor Spesial
Yang saya maksud dengan vektor spesial adalah vektor yang elemen-elemennya memang spesial dan unik. Ada 4 vektor spesial yang kita diskusikan di sini.
4.1. Vektor Nol
Vektor nol adalah vektor yang semua elemennya adalah angka nol. Vektor nol bisa dinotasikan dengan \(0\), sama dengan angka (skalar) \(0\) biasa. Oleh karena itu, apabila dijumpai angka \(0\) dalam sebuah teks, untuk membedakan apakah \(0\) ini adalah vektor atau skalar, anda perlu mengetahui konteks yang sedang dibicarakan dalam teks tersebut. Alternatif lain untuk menyatakan vektor nol adalah dengan menggunakan angka nol dengan subscript jumlah elemennya. Vektor nol yang terdiri dari \(n\) buah angka nol notasinya adalah \(0_n\). Contoh vektor nol adalah sebagai berikut,
\[0_4=\begin{pmatrix} 0,0,0,0\\ \end{pmatrix}\]4.2. Vektor Unit
Vektor unit, atau disebut juga vektor standar, adalah vektor yang semua elemen-nya adalah angka nol kecuali 1 elemen yang berupa angka satu. Vektor unit diidentifikasi dengan letak elemen angka satu-nya. Vektor unit ke-\(i\), dinotasikan dengan \(e_i\), adalah vektor yang elemen angka satu-nya merupakan elemen ke-\(i\) dari vektor tersebut. Contoh-contoh berikut menunjukkan vektor unit dengan 4 elemen,
\[e_1=\begin{bmatrix} 1\\ 0\\ 0\\ 0\\ \end{bmatrix}, \hspace{10pt} e_2=\begin{bmatrix} 0\\ 1\\ 0\\ 0\\ \end{bmatrix}, \hspace{10pt} e_3=\begin{bmatrix} 0\\ 0\\ 1\\ 0\\ \end{bmatrix}, \hspace{10pt} e_4=\begin{bmatrix} 0\\ 0\\ 0\\ 1\\ \end{bmatrix}\]Harap diperhatikan sekali lagi bahwa \(e_i\) adalah vektor, bukan notasi skalar yang berarti elemen ke-\(i\) dari vektor \(e\). Supaya tidak bingung, maka anda perlu melihat konteks di permasalahannya.
Vektor unit ke-\(i\) dengan \(n\) elemen dapat juga dideskripsikan dengan notasi yang lebih singkat dan padat, yaitu
\[(e_i)_j= \begin{cases} 1 \hspace{10pt} j=i\\ 0 \hspace{10pt} j\neq i \end{cases}\]untuk \(i,j=1,2,...,n\).
4.3. Vektor Satu
Vektor satu adalah vektor yang semua elemen-nya adalah angka satu. Untuk vektor satu yang memiliki \(n\) elemen, kita beri notasi \(\mathbf{1}_n\). Contohnya adalah sebagai berikut,
\[\mathbf{1}_4= \begin{pmatrix} 1,1,1,1\\ \end{pmatrix}\]4.4. Sparse Vector
Vektor spesial terakhir yang kita bahas di sini dinamakan sparse vector. Tidak saya terjemahkan ke bahasa Indonesia karena akan menjadi agak aneh. Kata “sparse” berarti jarang, sehingga sparse vector kalau diterjemahkan apa adanya akan menjadi “vektor jarang”. Aneh bukan? 😃
Vektor ini disebut sparse vector karena sebagian besar elemen-nya adalah nol, hanya sedikit sisanya yang bernilai bukan nol. Ke depan akan kita tunjukkan bahwa sparsity ini muncul di banyak hal.
5. Contoh-contoh Vektor
Jangan dibayangkan vektor hanya sebagai kumpulan angka-angka tak bermakna. Banyak sekali kondisi di dunia nyata yang bisa direpresentasikan dengan vektor. Di edisi ini kita akan melihat 3 contoh nyata representasi vektor dalam dunia nyata.
Contoh 1: Representasi Warna
Warna apapun bisa direpresentasikan dengan tiga warna dasar, yaitu merah (RED, disingkat R), hijau (GREEN, disingkat G), dan biru (blue, disingkat B), yang secara keseluruhan disingkat RGB. Warna apapun? Yes, warna apapun adalah kombinasi dari R, G, dan B dengan intensitas tertentu. Intensitas R, G, dan B bisa dinyatakan dengan nilai desimal antara 0 dan 1, atau dengan kombinasi bilangan heksadesimal, misalnya kombinasi enam bilangan heksadesimal, yang menghasilkan nilai antara #000000 (setara dengan nilai integer 0) dan #FFFFFF (setara dengan nilai integer 255). Jadi, RGB bisa dinyatakan dengan bilangan integer antara 0 dan 255. Berarti vektor nilai RGB untuk warna merah adalah \((255,0,0)\), vektor nilai RGB untuk warna hijau adalah \((0,255,0)\), dan vektor nilai RGB untuk warna biru adalah \((0,0,255)\). Untuk mengetahui vektor nilai RGB dari warna-warna lain, silakan bermain-main di sini.
Contoh 2: Nilai Ujian Mahasiswa
Misalnya, dalam satu kelas kecil ada 5 mahasiswa yang mengikuti perkuliahan. Di akhir perkuliahan, dosen mengadakan ujian untuk mengevaluasi tingkat pemahaman mahasiswa. Dari evaluasi tersebut, diketahui mahasiswa 1 mendapat nilai 70, mahasiswa 2 mendapat nilai 65, mahasiswa mendapat nilai 100, mahasiswa 4 mendapat nilai 80, dan mahasiswa 5 mendapat nilai 75. Nilai kelima mahasiswa ini dapat direpresentasikan dalam vektor berikut,
\[(70,65,100,80,75)\]Contoh 3: Perpindahan Benda
Vektor dapat juga digunakan untuk merepresentasikan perpindahan yang dialami oleh sebuah benda dalam ruang dua dimensi, sebagaimana ditunjukkan pada Gambar 1. Di Gambar 1, sebuah benda mengalami perpindahan sejauh \(x\). Oleh karena itu, kita merepresentasikan perpindahan ini dengan vektor \(x\). Proyeksi \(x\) di ruang 2 dimensi adalah \(x_1\) dan \(x_2\), maka vektor \(x\) dinyatakan dengan \(x=(x_1,x_2)\).
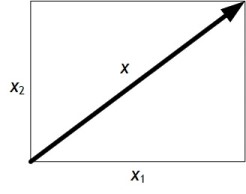
Dengan logika yang sama, vektor \(x\) bisa juga merepresentasikan perpindahan pada ruang berdimensi lebih tinggi. Misalnya, pada ruang tiga dimensi, vektor \(x\) kita akan menjadi \(x=(x_1,x_2,x_3)\), dan seterusnya.
Demikian pembahasan tentang dasar vektor. Semoga bermanfaat.
---
Blog archive: Years / Categories / Tags